Chia sẻ cách định giá cổ phiếu theo công thức của Benjamin Graham

Khoa học, nghệ thuật và phương pháp đánh giá cổ phiếu

Nếu bạn đưa cho 5 họa sĩ cùng 1 bộ bút vẽ, 1 bộ màu với yêu cầu vẽ về cùng 1 chủ đề, chắc chắn họ sẽ vẽ ra 5 bức tranh hoàn toàn khác nhau.

Với cổ phiếu cũng tương tự như vậy. Bộ bút vẽ là những công cụ, mô hình, dữ liệu… là những yếu tố định lượng.
Những nét vẽ, những ý tưởng và bức tranh cuối cùng thể hiện những yếu tố định tính.

Bài viết năm trong series hướng dẫn định giá cổ phiếu của GoValue. Chi tiết 7 Cách Định Giá Cổ Phiếu Chi Tiết [Có VD + file EXCEL]
Theo tôi, khái niệm quan trọng nhất về định giá cổ phiếu đó là:

Khái niệm #1: Định giá là 1 nghệ thuật

Khi bạn định giá 1 cổ phiếu, bạn phải đặt tất cả những con số, dữ liệu vào trong những mô hình.
Dựa trên những thông tin mà bạn có được về doanh nghiệp cả về quá khứ và những kế hoạch trong tương lai, bạn sẽ vẽ lên những bức tranh của riêng bạn về doanh nghiệp đó.
Những nét vẽ trong bức tranh đó chính là những giả định, những ý niệm chủ quan của bạn về cổ phiếu, doanh nghiệp đó.
Ở bước cuối cùng, bạn đặt tất cả những con số, những giả định đó vào 1 bức tranh tổng thể, và kết quả là bạn sẽ có được giá trị của doanh nghiệp.
Hay nói cách khác:

Giá cổ phiếu = Những con số trong quá khứ và hiện tại + Những giả định trong tương lai

Thêm vào đó, hầu hết mọi người thường mắc 1 sai lầm (kể cả rất nhiều bạn chuyên viên phân tích ở các công ty chứng khoán) đó là đưa ra 1 con số giá trị chính xác cho cổ phiếu.

Khái niệm #2: Giá trị cổ phiếu không phải là 1 con số mà là 1 khoảng giá trị

Từ những ví dụ mà tôi sẽ trình bày trong bài viết này ngay sau đây, một điều rất quan trọng mà bạn cần phải ghi nhớ, đó là giá trị cổ phiếu sẽ thay đổi theo từng kịch bàn và giả định trong tương lai mà bạn đưa vào.
Thay vì đặt quyết định đầu tư của mình vào duy nhất 1 con số, yếu tố khoa học và nghệ thuật được thể hiện ở đây, đó là bạn cần phải biết cách đặt các quyết định đầu tư của mình vào một “khoảng giá trị hợp lý”.
Bạn không thể nào biết trong tương lai, doanh nghiệp sẽ đi theo 1 kịch bản chắc chắn 100% nào. Điều này là hoàn toàn phi lý!
Do đó, hãy đánh giá cổ phiếu với nhiều kịch bản (thông thường là 3): kịch bản tích cực, kịch bản tiêu cực và kịch bản mà bạn kỳ vọng.
Khi đó, giá trị thực của cổ phiếu sẽ nằm ở đâu đó trong khoảng giá trị mà bạn xây dựng và tốt hơn hết bạn nên ra các quyết định mua bán dựa trên những khoảng giá trị này.

Hãy ghi nhớ 2 Khái niệm #1 #2 mà tôi vừa nhắc đến và bắt đầu với công thức của Benjamin Graham.

Sử dụng công thức Benjamin Graham để đánh giá cổ phiếu như thế nào?

Công thức định giá cổ phiếu của Benjamin Graham đã được nêu trong cuốn sách Nhà đầu tư thông minh (The Intelligent Investor) của ông.

Công thức này khá đơn giản và dễ sử dụng.

Theo tôi, đây là công thức đơn giản nhất mà không kém phần hiệu quả để bạn có thể sử dụng để có thêm 1 công cụ hữu hiệu, giảm thiểu được rất nhiều rủi ro trong quá trình đầu tư.

Công thức nguyên bản của Benjamin Graham

Công thức đầu tiên được Benjamin Graham công bố ở trong cuốn sách: Phân tích chứng khoán (Stock Analysis), cụ thể:

V = EPS x (8.5 + 2g)

Trong đó:

• V là giá trị của cổ phiếu
• EPS là thu nhập trên 1 cổ phiếu sau thuế lũy kế 12 tháng gần nhất
• 8.5 là tỷ lệ P/E ước tính của 1 cổ phiếu có tốc độ tăng trưởng thu nhập 0%
• g là tỷ lệ tăng trưởng kép bình quân trong 7 – 10 năm tới

Tuy nhiên, sau đó Ben Graham đã điều chỉnh lại công thức và thêm tỷ suất thu hồi vốn (required rate of return)

V = EPS x (8.5 + 2g) x 4.4 / y

Công thức này về cơ bản không có nhiều sự thay đổi, ngoại trừ Ben Graham đưa con số 4.4 là mức tỷ suất thu hồi vốn tối thiểu (hay, lãi suất phi rủi ro).

Tại năm 1962, khi Ben Graham công bố công thức này, lãi suất phi rủi ro tại Mỹ là khoảng 4.4% (tương đương lãi suất trái phiếu xếp hạng AAA kỳ hạn 20 năm).

Do đó, để điều chỉnh công thức cho hiện tại, cần thêm biến số Y là lãi suất phi rủi ro kỳ hạn 20 năm ở thời điểm hiện tại.

Tuy nhiên, hiện tại ở Việt Nam không có trái phiếu chính phủ kỳ hạn 20 năm để tham chiếu. Do đó, tôi thường sử dụng trái phiếu chính phủ kỳ hạn 10 năm + 0.5%.

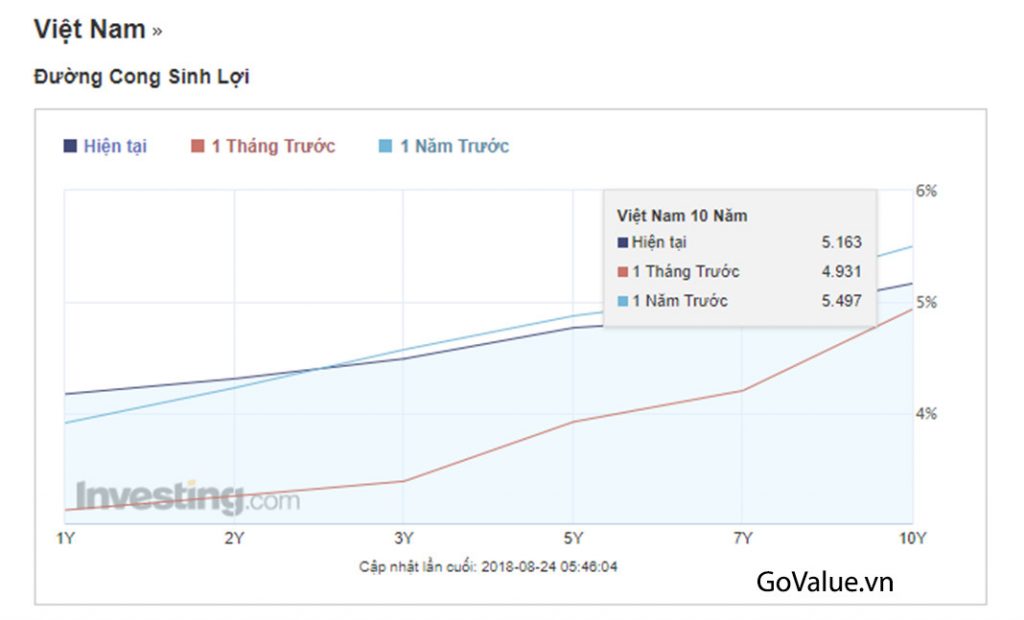
Bạn có thể lấy số liệu lãi suất trái phiếu chính phủ Việt Nam các kỳ hạn tại đây.

công thức của Ben Graham

Để có thể áp dụng công thức của Ben Graham một cách chính xác nhất, tôi thường sử dụng Normalized EPS, nghĩa là EPS đã được điều chỉnh đối với những khoản thu nhập bất thường hoặc được điều chỉnh giảm để phù hợp với diễn biến EPS của cổ phiếu trong 5 – 10 năm trước tùy thuộc vào từng cổ phiếu mà bạn đang đánh giá.

Việc điều chỉnh này là cần thiết bởi vì nếu chỉ đơn thuần lấy EPS theo báo cáo thì bạn sẽ dễ vướng vào những “cái bẫy” mà Ban lãnh đạo doanh nghiệp tạo ra.

Nói đơn giản, bạn phải hiểu rằng Ban lãnh đạo doanh nghiệp có hàng trăm phương thức kế toán có thể “phù phép” lợi nhuận và do đó EPS sẽ không đủ độ tin cậy để sử dụng.

Ngoài ra, trong những trường hợp mà lợi nhuận của doanh nghiệp biến động quá nhiều hàng năm, năm thì rất cao, năm thì rất thấp (có thể vì Ban lãnh đạo cố tình “xào nấu” báo cáo vì mục đích gì đó), khi đó, bạn không thể lấy con số EPS trailing 12M để đưa vào công thức của Ben Graham được.

Do đó, bạn cần nhìn lại diễn biến EPS của cổ phiếu trong khoảng 5 – 10 năm trước, điều chỉnh các khoản thu nhập bất thường, và “bình thường” hóa khoản EPS đó để có được mức EPS điều chỉnh cuối cùng để đưa vào công thức tính toán.

Đôi khi, nếu bạn không quá chắc chắn về số liệu EPS được báo cáo, sau khi điều chỉnh các khoản thu nhập bất thường, bạn có thể điều chỉnh giảm thêm 10-15% để tăng thêm mức độ thận trọng trong định giá, tùy thuộc vào mức nào đem đến cho bạn sự yên tâm nhất.

Điều chỉnh tỷ lệ tăng trưởng

Một điểm hạn chế trong công thức của Ben Graham là tỷ lệ tăng trưởng chiếm 1 tỷ lệ quá lớn trong giá trị doanh nghiệp.

Ví dụ: nếu doanh nghiệp được kỳ vọng tăng trưởng 10%/năm trong 5 năm tới thì hệ số nhân P/E khi tính giá trị của cổ phiếu sẽ khoảng 28x (cụ thể, 8 + 2 x 10). Điều này gần như là phi lý trong điều kiện thị trường hiện tại.

Do đó, tôi đưa thêm 2 điều chỉnh sau vào công thức của Ben Graham:

• Tôi đặt mức P/E cơ bản là 7 đối với 1 doanh nghiệp có tốc độ tăng trưởng 0% (thay vì P/E = 8 như trong công thức của Ben).
• Tôi áp dụng hệ số nhân 1x thay vì 2x đối với tốc độ tăng trưởng

Khi đó, công thức cuối cùng mà tôi sử dụng là:

V = Normalized EPS x (7 + g) x 4.4 / Y

Chú ý đối với tỷ lệ tăng trưởng

Đối với tỷ lệ tăng trưởng, bạn có thể sử dụng tỷ lệ tăng trưởng được các công ty chứng khoán ước lượng.

Tuy nhiên, bạn cũng nên đánh giá tỷ lệ tăng trưởng đó với tỷ lệ tăng trưởng EPS trong quá khứ (sau khi đã điều chỉnh các khoản thu nhập bất thường và tỷ lệ pha loãng cổ phiếu hàng năm).

Bạn nên chú ý rằng, một chu kỳ kinh doanh của 1 doanh nghiệp ở Việt Nam thường khoảng 7 năm.

Do đó, nếu EPS của cổ phiếu đã có tốc độ tăng trưởng bình quân ~ 20 – 25%/năm trong 3-5 năm gần nhất, thì khi đó tốc độ tăng trưởng bình quân khoảng 8-10%/năm trong 5 năm tiếp theo sẽ là hợp lý hơn.

Nếu các công ty chứng khoán vẫn ước lượng tốc độ tăng trưởng 20%/năm trong 5 năm tới thì có lẽ bạn chỉ nên tin vào đánh giá của mình.

Chú ý đối với lãi suất phi rủi ro

Một điểm rất hay trong công thức của Ben Graham là đưa vào lãi suất phi rủi ro hiện tại Y (%).

Theo như công thức, bạn có thể dễ dàng thấy giá trị của cổ phiếu tỷ lệ nghịch với lãi suất, hay hiểu đơn giản hơn, nếu lãi suất trái phiếu chính phủ tăng thì giá trị của doanh nghiệp cũng tăng.

Do đó, trong thực tế, tôi khuyên bạn nên sử dụng lãi suất phi rủi ro kỳ vọng. Nghĩa là, lãi suất trái phiếu chính phủ kỳ vọng trong 1-2 năm tới.

Ví dụ, nếu lãi suất trái phiếu chính phủ kỳ hạn 10 năm hiện tại đang là 5% và bạn đánh giá mức lãi suất hiện tại đang là đáy dài hạn. Những yếu tố vĩ mô cho thấy lãi suất có thể tăng thêm khoảng 1-2% trong hơn 1 năm tới.

Khi đó, hệ số Y trong công thức của Ben Graham mà tôi sử dụng sẽ là:

Y = 5% (Lãi suất trái phiếu chính phủ kỳ hạn 10 năm)

+ 0.5% (Điều chỉnh cho trái phiếu chính phủ kỳ hạn 20 năm)

+ 1% (Điều chỉnh cho kỳ vọng tăng lãi suất)

Cuối cùng, Y = 6.5.

Áp dụng với cổ phiếu MWG (CTCP Thế giới di động)

MWG là 1 cổ phiếu tăng trưởng nhanh với 3 chuỗi cửa hàng chính: Thế giới di động, Điện máy xanh và Bách hóa xanh.

Từ 2014 đến 2017, MWG đã tăng trưởng EPS với tốc độ bình quân 44.2%/năm.

Tuy nhiên, đến cuối năm 2017, báo cáo của MWG cho thấy sự chững lại của chuỗi Thế giới di động thị trường điện thoại thông minh đã bão hòa.

Đồng thời, chuỗi Bách Hóa Xanh gặp nhiều vấn đề trong việc mở rộng cửa hàng, do đó chưa đạt điểm hòa vốn và vẫn đang bị lỗ. Điện Máy Xanh thì dự kiến đến hết 2018, sang 2019 cũng sẽ bão hòa.

Do đó, hầu hết các công ty chứng khoán đều dự báo tốc độ tăng trưởng của MWG sẽ chậm lại trong nhiều năm tới, chỉ còn khoảng 20%/năm.

Ở ví dụ này, để thận trọng, tôi giả định tốc độ tăng trưởng trong 5 năm tới của MWG sẽ chỉ đạt 12 – 15%/năm.

Các số liệu của MWG:

Normalized EPS: 7.880 VNĐ/cổ phiếu

g: 12 – 15%/năm

Y: 6.5

Khi đó, giá trị của MWG sẽ nằm trong khoảng: 102.000 – 117.300 VNĐ/cổ phiếu.

Bạn vẫn nhớ Khái niệm #2 chứ?

Giá trị của cổ phiếu là 1 khoảng giá trị và trong trường hợp này, dựa trên công thức Ben Graham điều chỉnh, giá trị của MWG sẽ nằm đâu đó trong khoảng 102.000 – 117.300 VNĐ/cổ phiếu (nên nhớ rằng chúng ta đã rất thận trọng trong việc đánh giá tỷ lệ tăng trưởng).

Đây là con số dựa trên báo cáo của MWG công bố vào cuối tháng 1/2018 và giá thị trường tại ngày 02/02/2018 đang là 131.000 VNĐ/cổ phiếu.

Điều đó có nghĩa là thị trường đang định giá khá cao giá trị nội tại của MWG trong khoảng 5 năm tới.

Và bạn xem điều gì đã diễn ra với MWG sau đó:

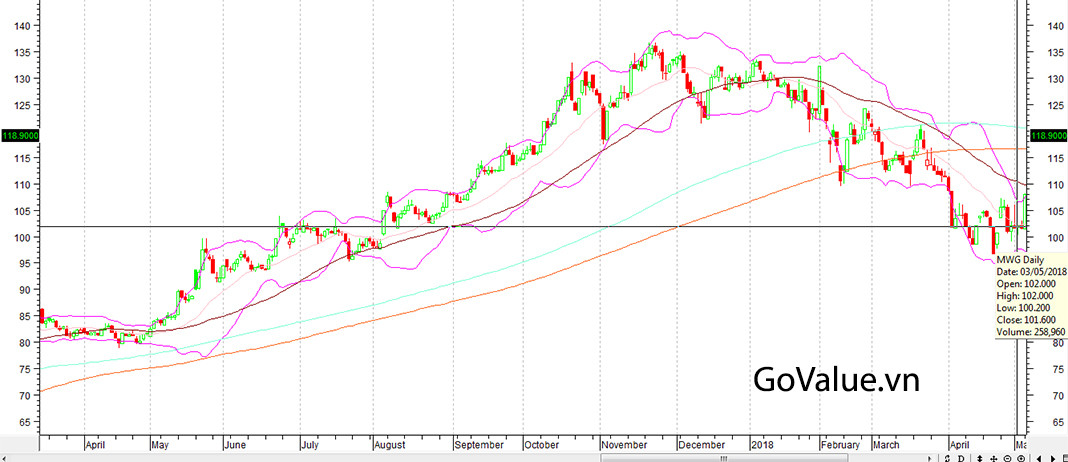
Giá của MWG đã giảm về mức dưới 100.000 VNĐ/cổ phiếu trong tháng 5/2018 và sau đó hồi lại ở mức khoảng 118.000 VNĐ/cổ phiếu, rất gần với mức định giá trước đó của chúng ta.

Như vậy, sau khoảng 6 tháng kể từ ngày chúng ta định giá theo công thức Ben Graham dựa trên báo cáo công bố của MWG, giá thị trường đã phản ánh vào giá trị cổ phiếu.

Nếu chúng ta bỏ chút ít thời gian ra đánh giá lại MWG, có thể chỉ bằng công thức đơn giản của Ben Graham thôi, chúng ta đã tránh được 1 đợt giảm giá khoảng 30% của MWG.

Như vậy, việc áp dụng công thức của Ben Graham có hiệu quả hay không? Điều này có lẽ bạn nên thử nghiệm vào tự có câu trả lời cho mình.

Tôi nghĩ, sẽ không mất gì nếu bạn trang bị cho mình 1 công thức hiệu quả và đơn giản nữa trong quá trình đầu tư.

Áp dụng công thức Ben Graham theo hướng tư duy “ngược”

Một điểm rất hay nữa của công thức Ben Graham là bạn có thể tính toán ngược lại để trả lời câu hỏi:

“Thị trường đang đánh giá tốc độ tăng trưởng EPS của cổ phiếu đó là bao nhiêu?”

Ví dụ, đối với MWG, với mức giá 131.000 VNĐ/cổ phiếu ngày 02/02/2018, tính toán ngược lại:

g = V x Y / (EPS x 4.4) – 7

Trong đó, ta giả định V = 131.000 VNĐ/cổ phiếu: g = 131.000 x 6.5 / (7.880 x 4.4) – 7, hay g = 17.56%/năm.

Khi đó, dựa trên những nghiên cứu và tìm hiểu của bạn về doanh nghiệp, bạn thấy rằng tỷ lệ tăng trưởng hợp lý chỉ có thể khoảng 12%/năm.

Như vậy, bạn có thể kết luận được thị trường đang đánh giá cao quá mức về tốc độ tăng trưởng của doanh nghiệp và đây là 1 dấu hiệu rõ ràng để bạn có thể bán ra hoặc giảm bớt tỷ trọng MWG.

Ngoài công thức Ben Graham, tôi cũng có những hướng dẫn cách đánh giá cổ phiếu bằng các phương pháp khác. Bạn có thể tham khảo những nội dung dưới đây:

Đầu tư chứng khoán cho người mới bắt đầu.